This article is Part 2 in a 5-Part Understanding Transformers Architecture.
Introduction
You might have probably encountered parameters like key_padding_mask, attn_mask etc.when using Pytorch’s MultiheadAttention layer. Similarly if you are using TransformerEncoderLayer, you can pass parameters like src_mask and src_key_padding_mask.
When using TransformerDecoder layer you’ll encounter even more parameters related to masking including tgt_mask, tgt_key_padding_mask.
In this post, I’ll demistify what these parameters are and how they are used internally. My goal is that after reading this post you are aware of importance of masking, and how to properly create masks as pass them to the models.
Note that I assume that you have some idea how attention is calculated. In the previous post, we implemented the “core” part of Transformers model, the Scaled Dot Product Attention function. However, we deliberately skipped how masking is used. Please refer to that post if you want a bit more context.
Masking padded tokens
When training or predicting, we typically pass a batch of data at once to the model rather than one by one. Let’s say we are classifying text into some categories and we have 3 sentences in our batch.
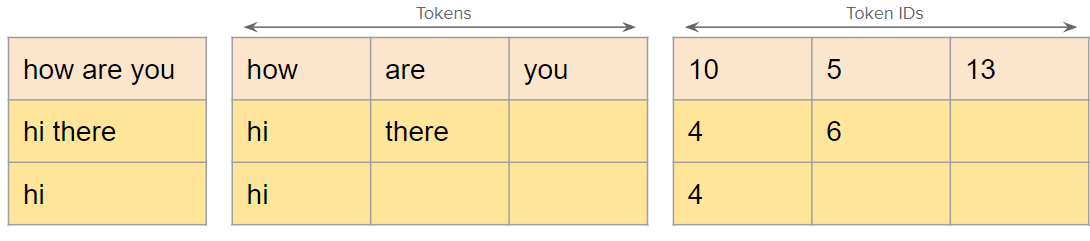
In this example, we have sentences of different lengths. We cannot create a a Pytorch Tensor using the token ids because, all of the rows must have same number of columns. So, in order to do this we “pad” the shorter sentences with a PAD token so that they all have same length as the longest one in the batch.
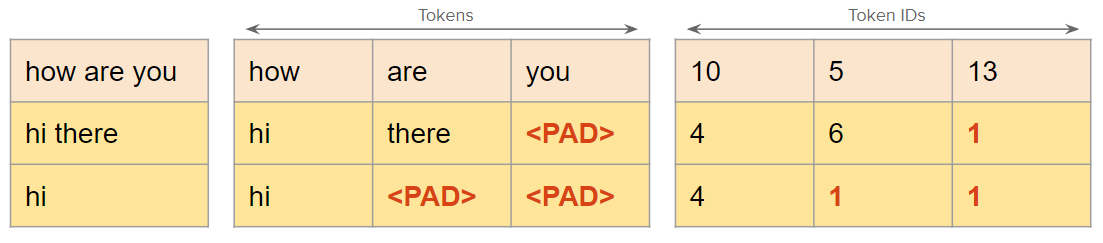
Now we have a batch of data with padded tokens as well. Padding was necessary just to create a tensor of token IDs that could be fed into the model. These PAD tokens serve no other purpose for our actual task of sentence classification or any other task for that matter.
Since they are useless and provide no meaningful information, the model should “ignore” such tokens. This is where the masks come in. We use masks to tell the model which are the actual tokens and should be considered by the model and which are the tokens which should be ignored.
As we see in the figure below, the mask is also a 2D matrix with same shape as token ids. The mask shown here a binary mask i.e a tensor with dtype=torch.bool. True value indicates that the token should be ignored.
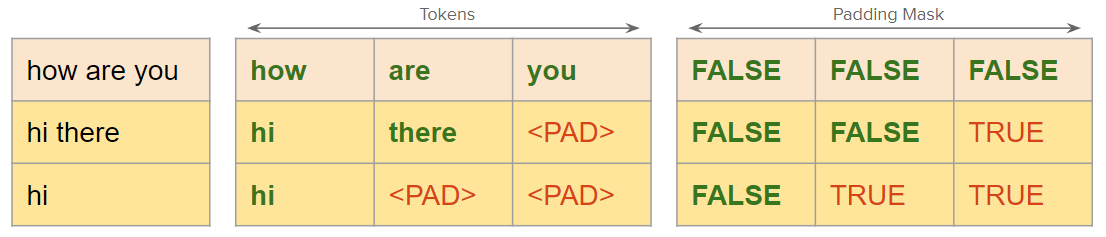
Note that, we can also define a float mask instead of binary mask. We’ll see later how the binary mask is actually converted to float mask and used by Pytorch. In Pytorch, when you want to use the mask for padded tokens, you need to provide it through the parameter called *_key_padding_mask. In the next section we’ll see how the mask is actually used by the model.
Before that, let’s also look at another situation where masking is necessary.
Causal Masked Self-Attention
Decoder models especially in tasks like causal language modeling, where the models generates text in an auto-regressive manner (i.e. predicts one token at a time), masking is essential while training.
Let’s look at how we structure the training process. Assume we have a single sentence in a batch “how are you”. Since our goal is to predict the next token, our simplified training process looks like the following.
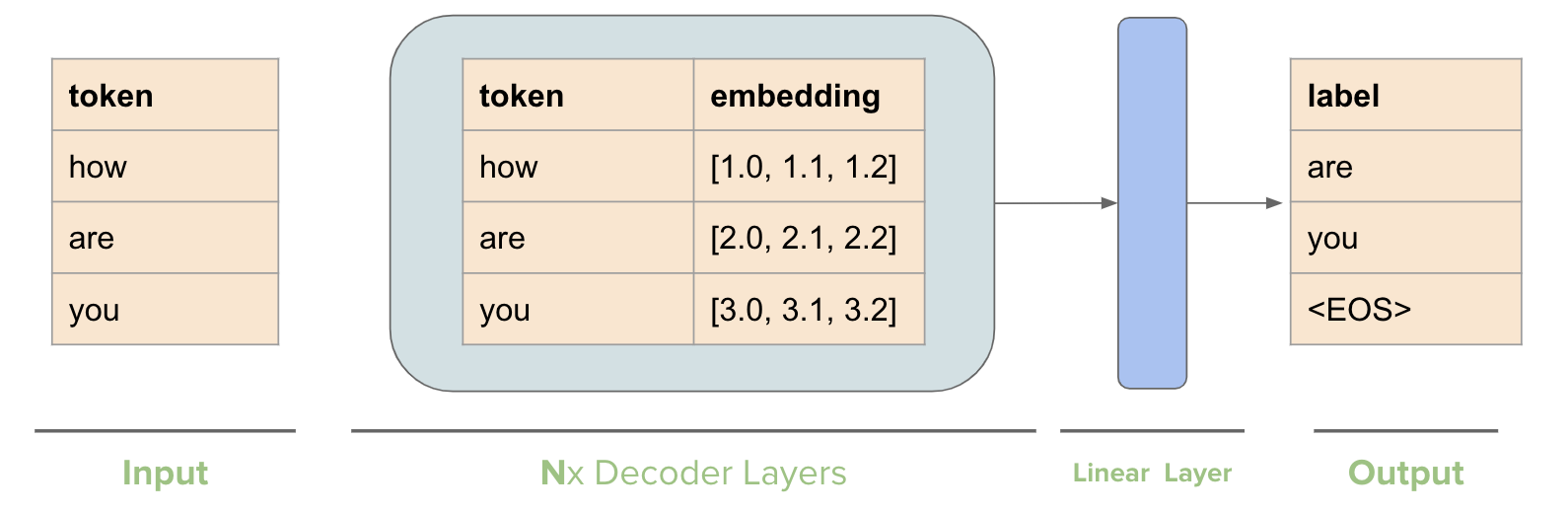
For each token we have a corresponding label which is the next token in the sequence. Now in the Multi-Head Attention layer, we compute the dot-product similarity between query and key i.e. \(QK^T\) as shown in the figure below.
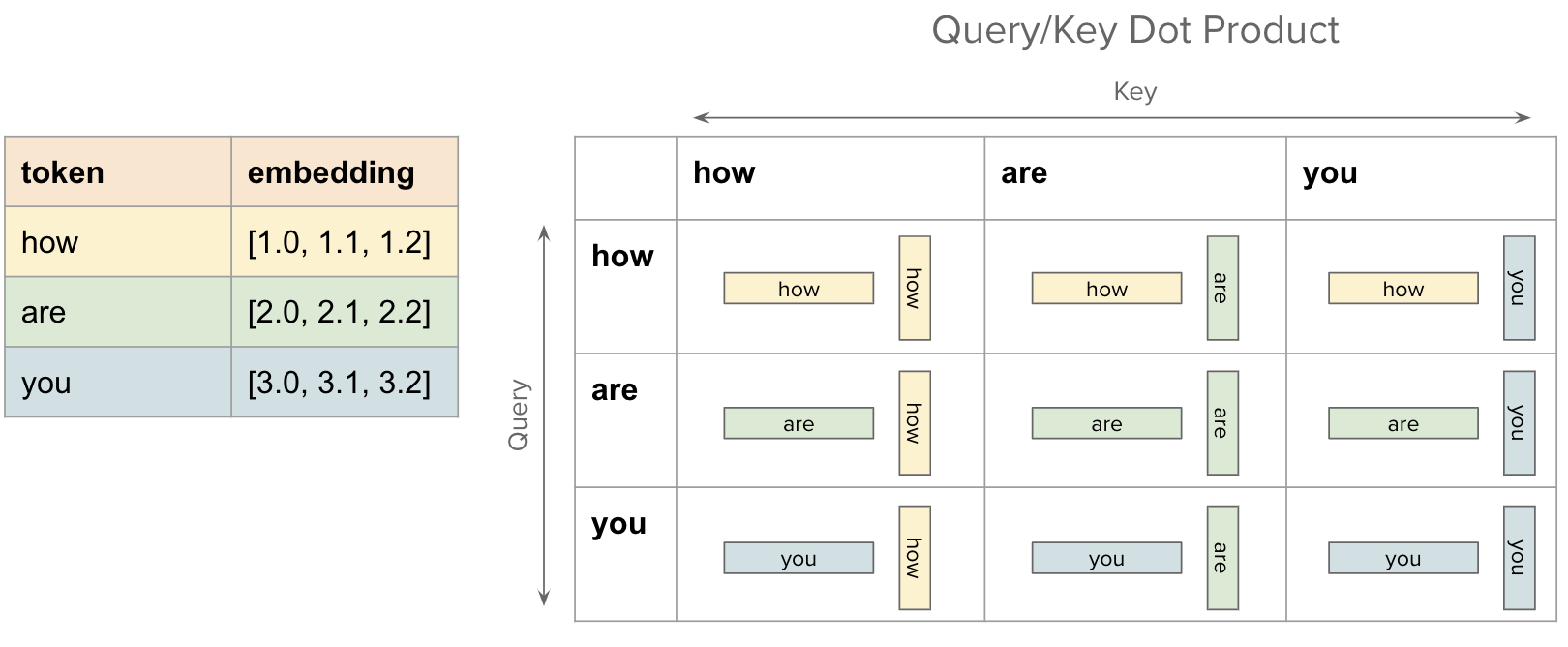
However, the problem is that for the token how, the label is are but when computing this dot-product similarity, the token how can also “see” the future tokens i.e. are and you. Same for the second token are. It can “see” the future token you.
This is a problem of data leakage and we should avoid it. The figure below shows the entries in this dot-product similarity matrix which are “invalid”.
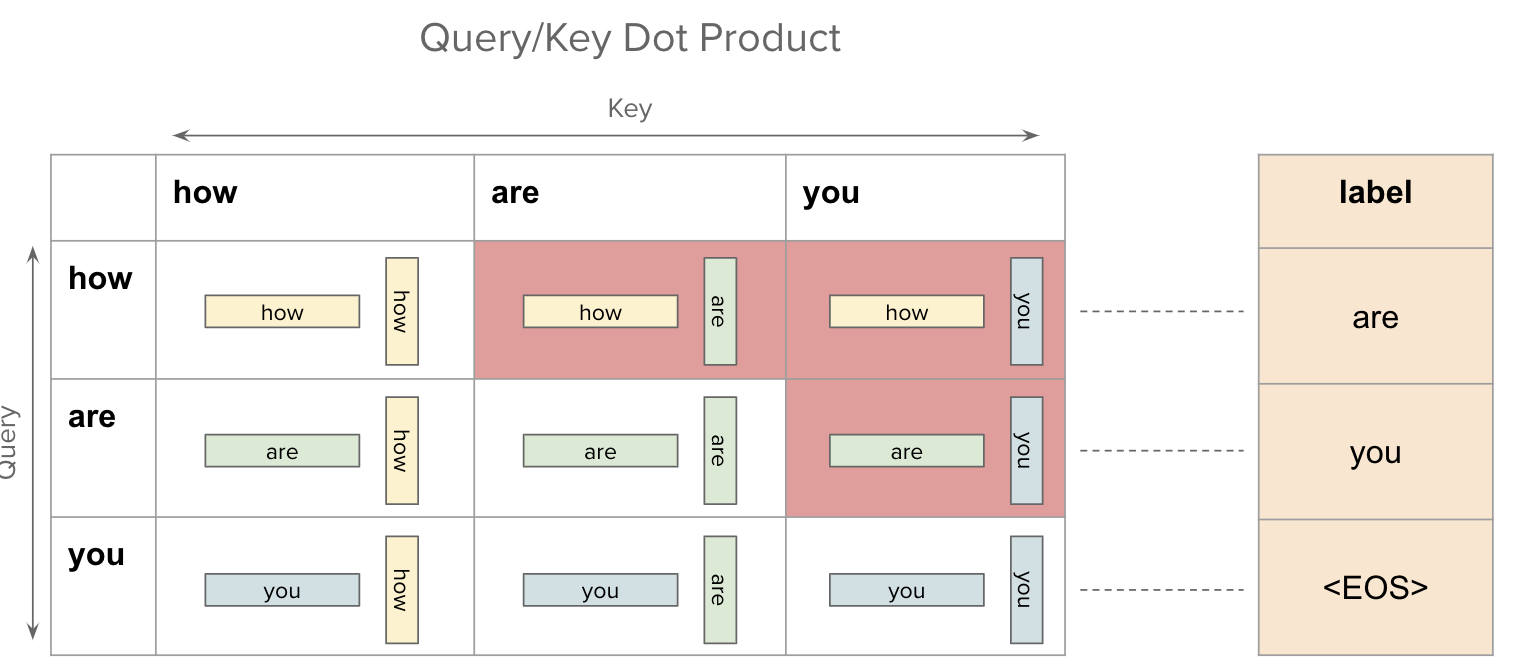
In order to fix this issue, we introduce “Attention Mask”. In the context of Decoders, this is also called “Masked Self-Attention”. The figure below shows how the attention mask looks like.
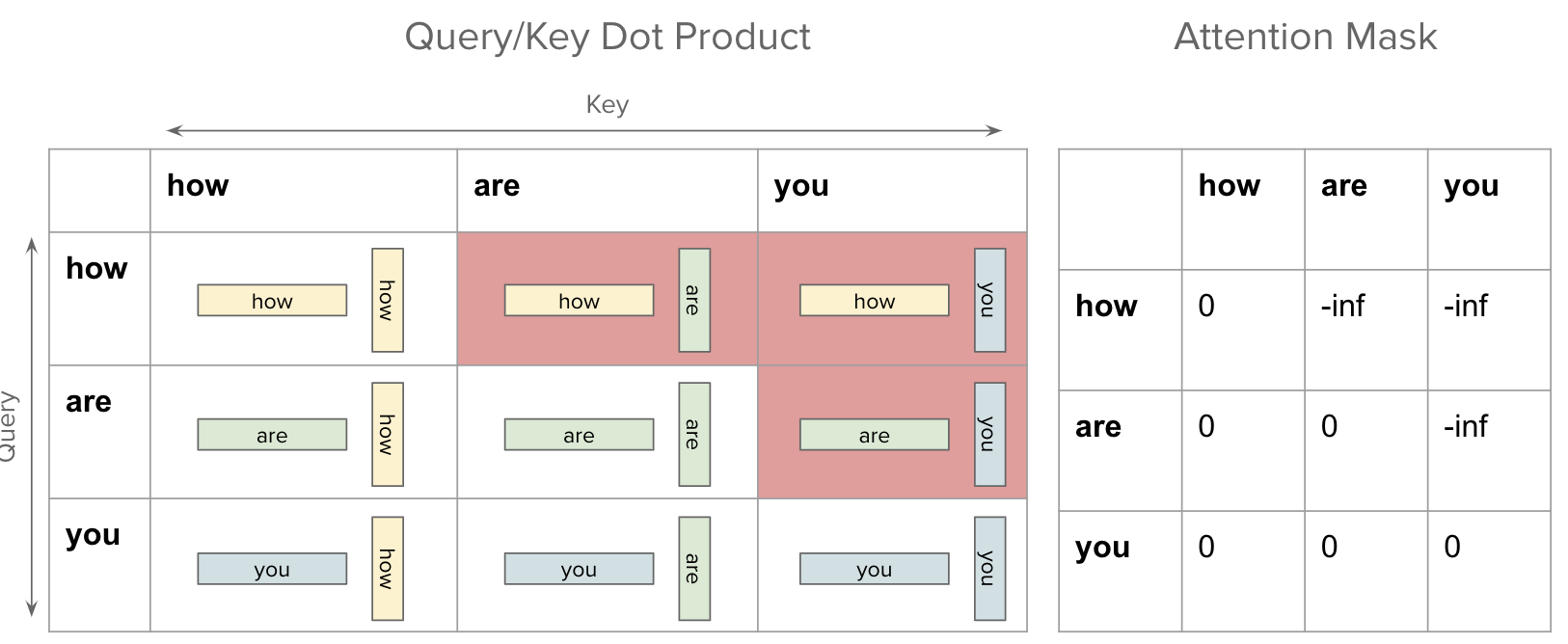
The mask has a value of negative infinity for “invalid” entries. Now, this mask is added to the dot-product similarity matrix before we apply the softmax function. For valid entires, we just add zero so the original dot product between query and key does not change, but for invalid entries, the new value will be negative infinity.
Here is the intuition: When a dot product of two vectors is higher, we consider them to be similar but so when two vectors have a dot product of negative infinity, then they are “infinitely dissimilar”.
How it is used
⚠️ In Pytorch scaled_dot_product_attention function when a boolean mask is passed to
attn_maskparameter, a value of True indicates that the element should take part in attention. However in MultiHeadAttention Layer,TransformerEncoderLayerandTransformerDecoderLayerfor a binary mask, a True value indicates that the corresponding key value will be ignored for the purpose of attention. Not sure why they implemented it differently, but I will consider True value to be ignored during attention calculation.
Let’s first see what the output of Pytorch’s MultiHeadAttention layer looks like.
1
2
3
4
5
6
7
8
9
10
11
12
13
import torch
embed_dim = 4
mha = torch.nn.MultiheadAttention(embed_dim=embed_dim, num_heads=1, batch_first=True)
# assume we have a batch of 2 sentences. 1st has 3 tokens and 2nd has 2 tokens
embeddings = torch.normal(mean=0, std=1, size=(2, 3, embed_dim))
# create a padding mask with all zeros so that every token is valid by default
key_padding_mask = torch.zeros(size=(2, 3), dtype=torch.bool)
# 3rd token of second sentence is a pad token
key_padding_mask[1, 2] = 1
_, torch_attn_mask = mha(embeddings, embeddings, embeddings, key_padding_mask=key_padding_mask)
print(torch_attn_mask)
1
2
3
4
5
6
7
8
9
10
tensor([
# attention weights for tokens in first sentence
[[0.2176, 0.4359, 0.3465],
[0.5966, 0.1536, 0.2498],
[0.4046, 0.2353, 0.3600]],
# attention weights for tokens second sentence
[[0.5787, 0.4213, 0.0000],
[0.4964, 0.5036, 0.0000],
[0.5379, 0.4621, 0.0000]]], grad_fn=<MeanBackward1>)
I’ve printed the attention mask produced by the MHA layer. As we specified that the last token of 2nd sentence is a PAD token, the attention weights for that token is 0 (3rd column of 2nd matrix). Since we take a weighted sum of Value vectors \(V_i\) using the attention weights, the embeddings of PAD tokens will not have any contribution.
For the first token in first sentence, the final embedding will be calculated as \(token1\_embeddings = 0.21*V_{token1} + 0.43*V_{token2} + 0.34 * V_{token3}\)
And for the first token in second sentence, the final embedding will be calculated as \(token1\_embeddings = 0.57*V_{token1} + 0.42*V_{token2} + 0 * V_{token3}\)
Note that the Value embeddings of \(token3\) in this case does not contribute at all since it becomes a zero vector after multiplying it with 0.
Let’s see how the mask is actually used internally. First we need to reshape our mask to proper shape. The key_padding_mask is 2D i.e. (batch_size, seq_len). But as we saw previously, we add the mask to the dot-product similarity. For this we need to create a 3D tensor (batch_size, seq_len, seq_len)
1
2
3
4
5
# reshape mask to proper shape
key_padding_mask_expanded = key_padding_mask.unsqueeze(1) # (bs, 1, seq_len)
# expand 3 times in the 2nd dimension since we have 3 tokens
key_padding_mask_expanded = key_padding_mask_expanded.expand(-1, 3, -1)
print(key_padding_mask_expanded)
1
2
3
4
5
6
7
8
9
10
tensor([
# mask for 1st sentence. every token is valid
[[False, False, False],
[False, False, False],
[False, False, False]],
# mask for 2nd sentence. last token is invalid
[[False, False, True],
[False, False, True],
[False, False, True]]])
We are basically copying the same padding mask for each sentence 3 times.
Now let’s use the mask before calculating the final attention weights.
1
2
3
4
5
6
7
8
# compute dot-product between Query and Key tokens
scores = embeddings @ embeddings.transpose(1, 2)
print(scores)
# where ever the mask value is True, fill the corresponding entry in scores to -inf
scores = scores.masked_fill(key_padding_mask_expanded, -torch.inf)
print(scores)
attn_weights = torch.softmax(scores, dim=-1)
print(attn_weights.round(decimals=2))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
# scores
tensor([[[ 1.5403, -2.2226, -0.4307],
[-2.2226, 7.0114, 2.7344],
[-0.4307, 2.7344, 2.9128]],
[[ 2.1827, -0.3097, -1.5490],
[-0.3097, 0.1501, 0.7644],
[-1.5490, 0.7644, 4.9995]]])
# add -inf to masked tokens
tensor([[[ 1.5403, -2.2226, -0.4307],
[-2.2226, 7.0114, 2.7344],
[-0.4307, 2.7344, 2.9128]],
[[ 2.1827, -0.3097, -inf],
[-0.3097, 0.1501, -inf],
[-1.5490, 0.7644, -inf]]])
# attention weights
tensor([
# attention weights for tokens in 1st sentence
[[0.8600, 0.0200, 0.1200],
[0.0000, 0.9900, 0.0100],
[0.0200, 0.4500, 0.5300]],
# attention weights fo tokens in 2nd sentence
[[0.9200, 0.0800, 0.0000],
[0.3900, 0.6100, 0.0000],
[0.0900, 0.9100, 0.0000]]])
As we see, the attention weights for the PAD token is 0 for the second sentence. Note that other attention weights are not same as the one from mha layer because mha passes the input embeddings through a linear layer which changes the values of embeddings. But that is not our concern. We are just making sure that the attention weights for the 3rd token is 0 in both the cases.
Here the important part is scores = scores.masked_fill(key_padding_mask_expanded, -torch.inf). This is same as the following.
1
2
3
4
5
scores = embeddings @ embeddings.transpose(1, 2)
# create a float_mask as I describe previously
float_mask = torch.zeros_like(key_padding_mask_expanded, dtype=torch.float32).masked_fill(key_padding_mask_expanded, -torch.inf)
# add the float mask to the scores and apply softmax function
print(torch.softmax(scores + float_mask, dim=-1).round(decimals=2))
This is all there is to it. Now let’s look at causal mask, which is also very easy to create. As mentioned above, the purpose of causal mask is to prevent attending to future tokens. So we can create this kind of mask using torch.triu function.
1
2
3
4
5
# we have 2 sentences and 3 tokens
causal_mask = torch.ones((2, 3, 3), dtype=torch.bool)
causal_mask = torch.triu(causal_mask, diagonal=1)
print(causal_mask)
print(mha(embeddings, embeddings, embeddings, attn_mask=causal_mask)[1])
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# causal mask
tensor([[[False, True, True],
[False, False, True],
[False, False, False]],
[[False, True, True],
[False, False, True],
[False, False, False]]])
# attention weights
tensor([
# attention weights for tokens in 1st sentence
[[1.0000, 0.0000, 0.0000],
[0.7953, 0.2047, 0.0000],
[0.4046, 0.2353, 0.3600]],
# attention weights for tokens in 2nd sentence
[[1.0000, 0.0000, 0.0000],
[0.4964, 0.5036, 0.0000],
[0.3736, 0.3210, 0.3054]]], grad_fn=<MeanBackward1>)
As we see, the weights for future tokens are 0. This way these future tokens have no influence when calculating the embeddings of the current token. There is also a helper function in Pytorch that you can use to easily generate this kind of mask.
1
2
causal_mask = torch.nn.Transformer.generate_square_subsequent_mask(sz=3) # we have 3 tokens, so size=3
print(mha(embeddings, embeddings, embeddings, attn_mask=causal_mask)[1])
which returns the following which is exactly the same as before.
1
2
3
4
5
6
7
tensor([[[1.0000, 0.0000, 0.0000],
[0.7953, 0.2047, 0.0000],
[0.4046, 0.2353, 0.3600]],
[[1.0000, 0.0000, 0.0000],
[0.4964, 0.5036, 0.0000],
[0.3736, 0.3210, 0.3054]]], grad_fn=<MeanBackward1>)
Conclusion
We explored how masks are used internally when calculating attention. For most of the cases, we can just create a binary mask and pass it to the layers. Internally it will be converted to float mask and will be added to the dot-product similarity between Query and Key tokens before passing it to the softmax function.
I hope you found this post useful. Please let me know if you find any errors.
This article is Part 2 in a 5-Part Understanding Transformers Architecture.




Comments